Модуль упругости меди
Модуль упругости меди
Модуль Юнга
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.
Это свойство любого материала, и оно зависит от температуры и оказываемого давления.
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.
Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.
Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.
Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.
Примеры значений модуля Юнга (упругости) для:
- (т.е. для резины он в 5 раз меньше стали)
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
|---|---|
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):

- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
- Fупр — сила упругости
- k × Δl — удлинение тела
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
- l = 2,5 м
- F = 50 H
- E = ?
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Модуль упругости меди

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
СОСУДЫ И АППАРАТЫ
ИЗ ЦВЕТНЫХ МЕТАЛЛОВ
НОРМЫ И МЕТОДЫ РАСЧЕТА НА ПРОЧНОСТЬ.
ОБЩИЕ ТРЕБОВАНИЯ
ГОСТ 26158-84
(СТ СЭВ 4007-83)
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
СОСУДЫ И АППАРАТЫ ИЗ ЦВЕТНЫХ МЕТАЛЛОВ
Нормы и методы расчета на прочность.
Общие требования
Vessels and apparatus of non-ferrous metals. Norms and methods of strength calculation. General requirements
ГОСТ
26158-84
(СТ СЭВ 4007-83)
Постановлением Государственного комитета СССР по стандартам от 18 апреля 1984 г. № 1337 срок введения установлен
1. Настоящий стандарт распространяется на сосуды и аппараты из алюминия, меди и их сплавов, предназначенные для работы в химической, нефтеперерабатывающей и смежных отраслях промышленности.
Стандарт устанавливает нормы и общие требования к методам расчета на прочность конструктивных элементов сосудов и аппаратов, работающих при статических нагрузках под внутренним избыточным давлением и под действием осевых и поперечных усилий и изгибающих моментов, а также устанавливает значения допускаемых напряжений, модулей продольной упругости материалов, коэффициентов прочности сварных и паяных швов.
Нормы рассчитаны на условия, устанавливаемые «Правилами устройства и безопасной эксплуатации сосудов, работающих под давлением», утвержденными Госгортехнадзором СССР, и при условии, что отклонения от геометрической формы и неточности изготовления рассчитываемых элементов сосудов и аппаратов не превышают допусков, установленных нормативно-технической документацией на сосуды и аппараты из алюминия, меди и их сплавов.
Стандарт полностью соответствует СТ СЭВ 4007-83.
2. Расчетную температуру определяют по ГОСТ 14249-80, разд. 1.
3. Рабочее, расчетное и пробное давление определяют по ГОСТ 14249-80, разд. 1.
4. За расчетные усилия и моменты принимают действующие в состоянии нагружения (например, при эксплуатации, испыта нии или монтаже) усилия и моменты, возникающие в результате действия собственного веса, присоединительных трубопроводов, снеговой и других временных нагрузок. Расчетные усилия и моменты от ветровой нагрузки и сейсмических воздействий определяют по ГОСТ 24756-81.
5. Допускаемые напряжения и коэффициенты запаса прочности
5.2. Допускаемое напряжение [ s ], МПа (кгс/см 2 ), для материалов, не приведенных в приложении 1 , определяют по формуле:
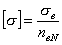 , (1)
, (1)
где s в — минимальное значение временного сопротивления при расчетной температуре, МПа (кгс/см 2 );
n в N — коэффициент запаса прочности по временному сопротивлению при отсутствии данных о пределе длительной прочности.
5.3. При наличии данных о пределе длительной прочности при расчетной температуре допускаемое напряжение для цветных металлов, за исключением алюминиевых литейных сплавов, допускается определять по формуле:
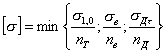 , (2)
, (2)
где s 1,0 — минимальное значение условного предела текучести при 1 %-ном остаточном удлинении при расчетной температуре, МПа (кгс/см 2 );
пТ — коэффициент запаса прочности по условному пределу текучести;
пв — коэффициент запаса прочности по временному сопротивлению при наличии данных о пределе длительной прочности;
s дт — среднее значение предела длительной прочности за время t часов при расчетной температуре, МПа (кгс/см 2 );
n д — коэффициент запаса прочности по пределу длительной прочности.
5.4. При отсутствии данных об условном пределе текучести при 1 %-ном остаточном удлинении используют значение условного предела текучести при 0,2 %-ном остаточном удлинении.
5.5. Коэффициенты запаса прочности для различных материалов, используемые при расчетах в зависимости от условий нагружения, должны соответствовать приведенным в таблице.
Модуль упругости (Модуль Юнга)
Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.
Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.

Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.
Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
 Опыт с пружинными весами
Опыт с пружинными весами
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
- Через касательные напряжения (τz) и угол сдвига (γ):
- Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.
 Определение модуля упругости щебеночного основания
Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
Модуль упругости различных материалов
Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:
- природы веществ, формирующих состав материала;
- моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
- структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
- плотности материала (распределения частиц в его объеме);
- обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).
Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.
Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:
- бронза – 10,4 ГПа;
- алюминиевая бронза при литье – 10,3 ГПа;
- фосфористая бронза катанная – 11,3 ГПа.
Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.
Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:
- литая – 82 ГПа;
- прокатанная – 108 ГПа;
- деформированная – 112 ГПа;
- холоднотянутая – 127 ГПа.
Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.
Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.
Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.
 Модули упругости некоторых материалов
Модули упругости некоторых материалов
На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:
- его диаметр;
- шаг свивки;
- угол свивки.
Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.
Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.
Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.
Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.
Как определить модуль упругости стали
Выяснить модули упругости для различных марок стали можно несколькими путями:
- по справочным данным из таблиц;
- экспериментальными методами для небольшого образца;
- расчетными методами, зная необходимые данные.
Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.
Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.
В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.
| Сталь | Модуль (Е), ГПа |
| углеродистая | 195-205 |
| легированная | 206-235 |
| Ст.3, Ст.5 | 210 |
| сталь 45 | 200 |
| 25Г2С, 30ХГ2С | 200 |
Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.
Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.
В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:
Расчеты ведут в мм и МПа.
Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
- Виды нагрузок
- Понятие о модуле упругости
- Таблица 1: Модуль упругости для металлов и сплавов
- Модуль упругости для разных марок стали
- Таблица 2: Упругость сталей
- Модули прочности
- Таблица 3: Модули прочности для сталей
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
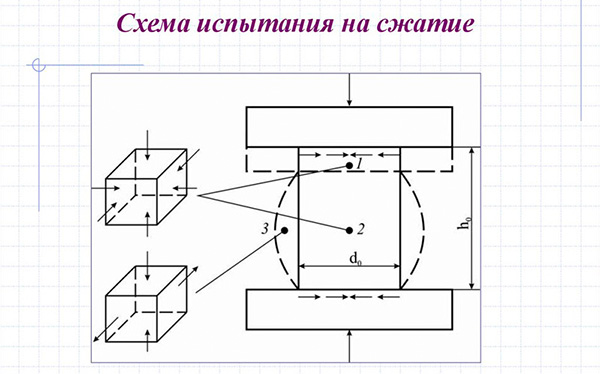
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
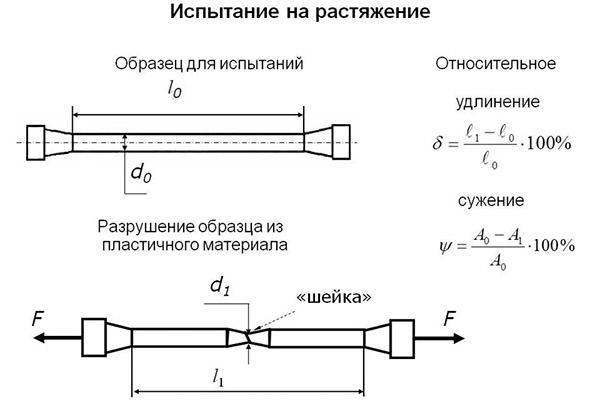
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
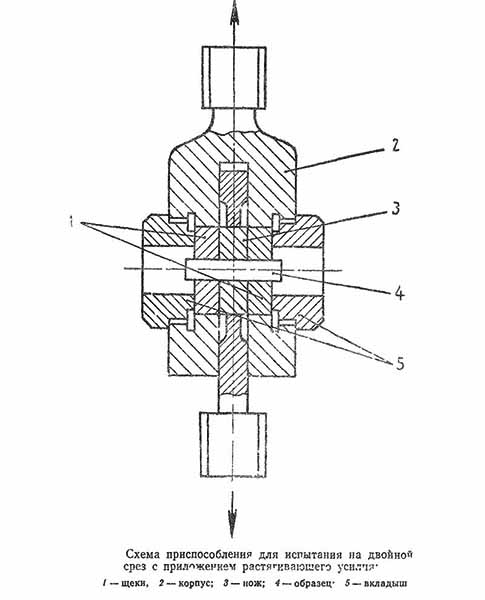
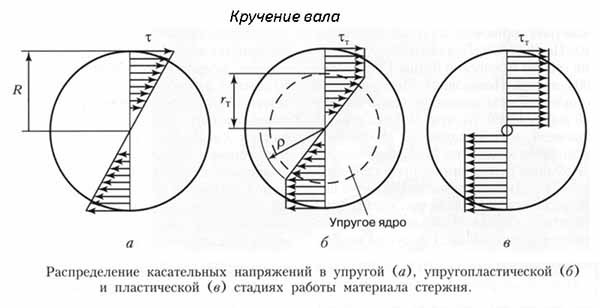
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
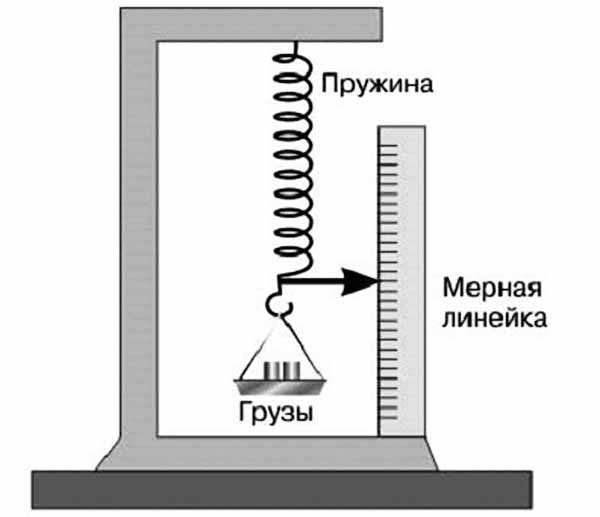
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Расчетные сопротивления и модули упругости
для строительных материалов
| расчетные сопротивления строительных материалов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
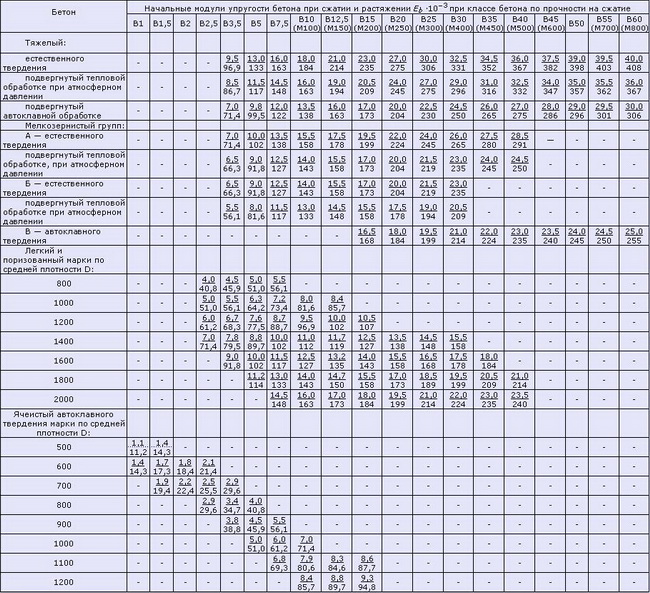
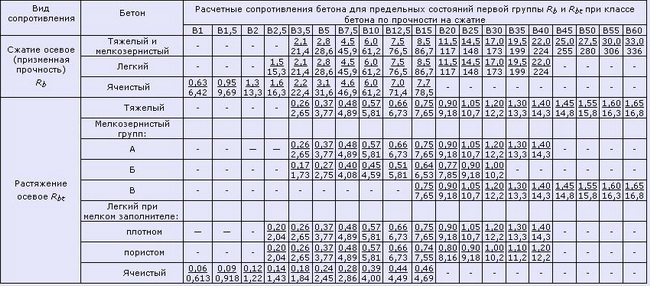
Нормативные данные для рассчетов железобетонных конструкцийТаблица 2. Модули упругости бетона (согласно СП 52-101-2003)
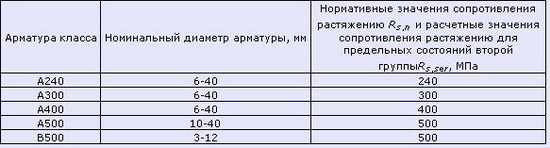
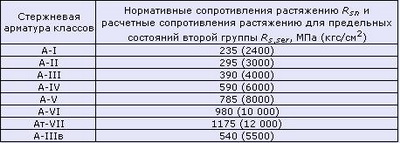
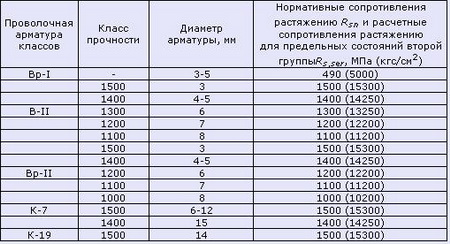
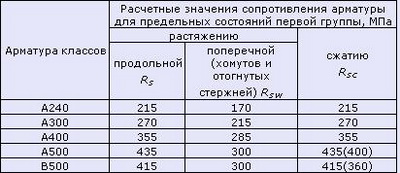
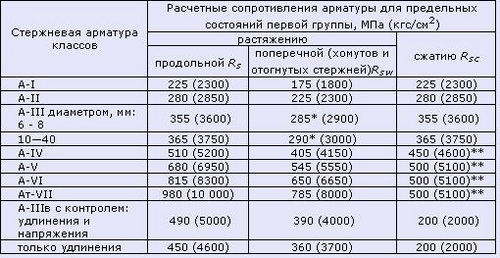
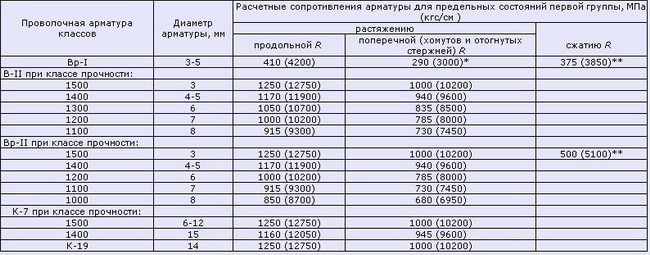
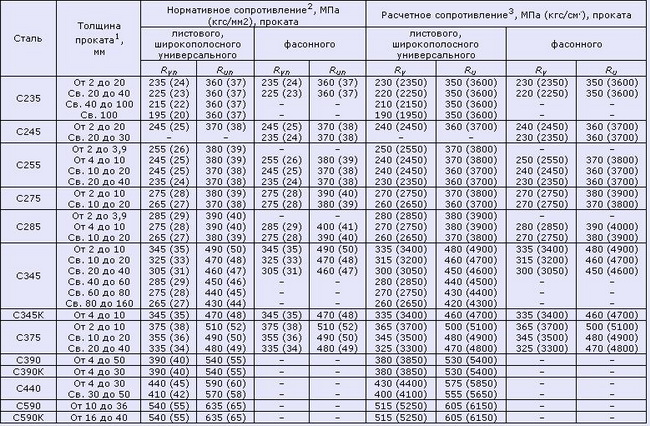
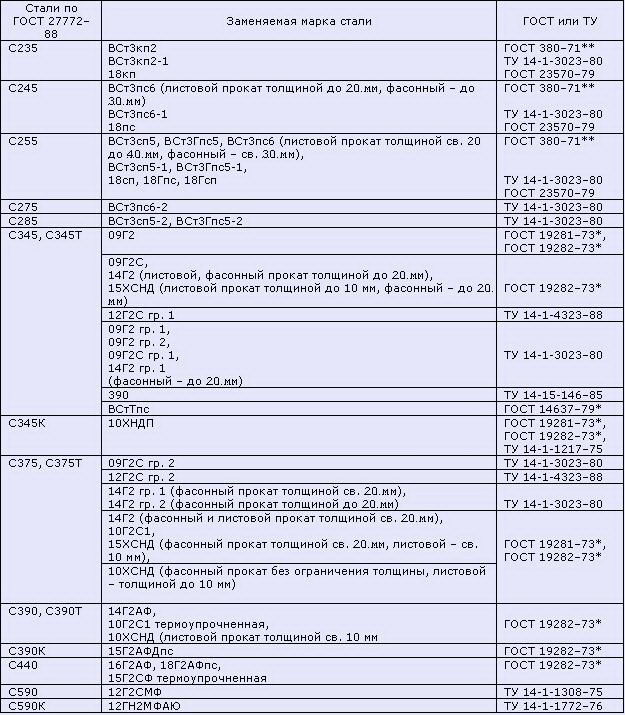
Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996) Примечания: Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003) Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003) Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996) Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003) Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003) Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996) Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996) Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003) Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996) Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996) Нормативные данные для расчетов металлических контрукцийТаблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений Примечания: Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990)) Примечания: Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны. 7.5. Сопротивление материалов
Модуль Юнга численно равен напряжению, увеличивающему длину образца в два раза: для стали, Ест = (2,0-2,2)×10 5 МПа; для чугуна, Еч = 1,2×10 5 МПа; Закон Гука: возникающее удлинение образца Δl под действием внешней силы Р пропорционально величине действующей силы, первоначальной длине l и обратно пропорционально площади поперечного сечения S: Δl = (l × Р) / (Е × S) или р = Е × ε, где р = Р / S — напряжение; ε = Δl / l — относительная продольная деформация. Материалы разделяются на хрупкие и пластичные. Хрупкие вещества Совместно с деформацией растяжения наблюдается уменьшение диаметра образца. Если Δd — изменение диаметра образца, то ε1 = Δd / d принято называть относительной поперечной деформацией. Абсолютная величина μ = ε1 / ε носит название коэффициента поперечной деформации — коэффициента Пуассона. Коэффициент Пуассона для стали: μст = 0,3. Сдвиг — деформация, при которой все слои тела, параллельные некоторой плоскости, смещаются друг относительно друга. Закон Гука для деформации сдвига: р = G × α, где G — модуль сдвига; Соотношение между упругими постоянными: G = Е / 2 × (1 + μ). Температурный коэффициент линейного расширения — величина, равная среднему (в интервале температур [0; t] °С) относительному удлинению тела (град -1 ): α = (l1 – l) / (t × l0). Температурный коэффициент линейного Отсутствие тепловых зазоров приводит к возникновению значительных сил, определяемых площадью сечения вала: где E — модуль Юнга, МПа; S — площадь сечения вала, м 2 ; α — коэффициент линейного расширения, град -1 ; Δt — повышение температуры, °С. Предел текучести — напряжение, при котором появляется текучесть (увеличение деформации без увеличения деформирующей силы). Предел текучести: рядовая сталь, σт = 200 МПа; сталь средней прочности, σт = 400 МПа; легированная сталь, σт = 800 МПа. Предел упругости — напряжение, при котором остаточные деформации впервые достигают некоторой величины, характеризуемой определенным допуском, устанавливаемым техническими условиями. Предел прочности — напряжение, отвечающее наибольшей нагрузке, Усталость — процесс постепенного возникновения и развития трещины в материале под воздействием многократно повторяющихся силовых Предел выносливости — наибольшее напряжение, которое может выдержать материал при заданном числе циклов нагружения. Ползучесть — нарастание во времени пластической деформации материала при силовых воздействиях, меньших чем те, которые вызывают остаточную деформацию. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- Гидродинамическая прочистка канализации: решение засоров
- Служба по дезинфекции: практические решения для дома и бизнеса
- Практическое применение средств индивидуальной защиты на работе
- Преимущества гидроструйной очистки поверхностей
- Армированная полиэтиленовая пленка для теплиц — как продлить срок службы



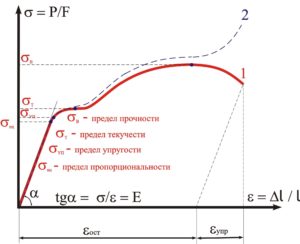 Модуль Юнга (модуль упругости первого рода) Е, МПа, Н/мм 2 — постоянная упругости в законе Гука в пределах, когда деформация пропорциональна напряжению.
Модуль Юнга (модуль упругости первого рода) Е, МПа, Н/мм 2 — постоянная упругости в законе Гука в пределах, когда деформация пропорциональна напряжению.