Формула Томсона: объяснение и применение

Формула Томсона, также известная как формула Лармора, описывает частоту колебаний LC-контуров, а также используется для определения резонансной частоты электрических колебательных систем. Она была названа в честь английского физика Уильяма Томсона, также известного как лорд Кельвин. В данной статье мы рассмотрим суть и применение формулы Томсона, а также её значение в различных областях электроники.

Основы Формулы Томсона

Формула Томсона выражается следующим образом:

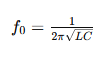
Где:

( f_0 ) — резонансная частота контура,
( L ) — индуктивность контура (Генри),
( C ) — ёмкость конденсатора (Фарад).

Формула показывает, что резонансная частота зависит от индуктивности и ёмкости контура. Она используется для расчёта частоты, при которой колебательная система достигает резонанса, что приводит к максимальной амплитуде колебаний.

Применение Формулы Томсона

Радиоэлектроника: Формула используется для настройки радиоприёмников и передатчиков на нужную частоту.
Контурные фильтры: Применяется для проектирования фильтров, которые могут избирательно пропускать сигналы определённых частот.
Резонансные преобразователи: В схемах, где требуется максимальная передача энергии на резонансной частоте, формула Томсона помогает рассчитать оптимальные параметры.

Пример расчёта

Рассмотрим пример расчёта резонансной частоты контура с индуктивностью ( L = 10 ) мГн и ёмкостью ( C = 100 ) нФ.

Подставим значения в формулу:

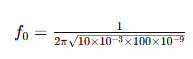
Выполним вычисления:

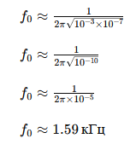
Сравнение с другими методами расчёта

Метод	Преимущества	Недостатки
Формула Томсона	Простота, высокая точность	Ограничения на типы контуров
Экспериментальные	Высокая точность при сложных схемах	Трудоёмкость, зависимость от условий
Численные методы	Подходит для нелинейных систем	Требует вычислительных ресурсов

Формула Томсона является важным инструментом в электронике, особенно в радиоэлектронике и проектировании резонансных систем. Она позволяет точно определить резонансную частоту LC-контуров, что крайне важно для настройки и оптимизации различных устройств. Понимание и использование этой формулы обеспечивает надёжную и эффективную работу колебательных систем.